Area Of A Circle Units

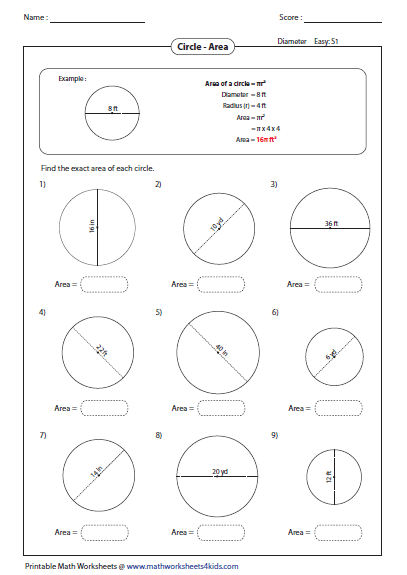
Calculating areas and circumferences of circles plays an important role in almost all field of science and real life. For instance, formula for circumference and area of a circle can be applied into geometry. They are used to explore many other formulas and mathematical equations. An arch length is a portion of the circumference of a circle.

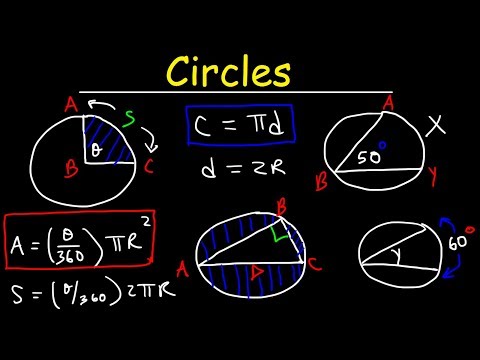
The ratio of the length of an arc to the circumference is equal to the ratio of the measure of the arc to $360$ degrees. A sector of a circles is the region bounded by two radii of the circle and their intercepted arc. Session 6 Area Learn that area is a measure of how much surface is covered. Explore the relationship between the size of the unit used and the resulting measurement. Find the area of irregular shapes by counting squares or subdividing the figure into sections.

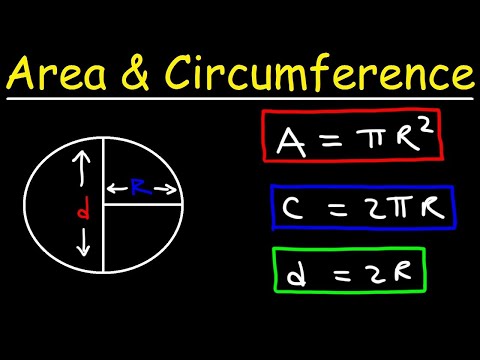
Learn how to approximate the area more accurately by using smaller and smaller units. Relate this counting approach to the standard area formulas for triangles, trapezoids, and parallelograms. This concept can be of significance in geometry, to find the perimeter, area and volume of solids. Since area is a measure of two dimensions, you always report area in square units like square inches or square feet . This is especially important when calculating the area of a circle for an assignment since an answer without correctly reported units is likely incorrect or incomplete. When the length of the radius or diameter or even the circumference of the circle is already given, then we can use the surface formula to find out the surface area.

The surface is represented in square units. For any other value for the length of the radius of a circle, just supply a positive real number and click on the GENERATE WORK button. They can use these methods in order to determine the area and lengths of parts of a circle.

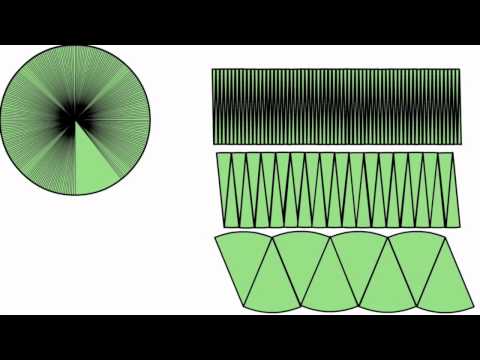
Why is the area of a circle pi times the square of the radius? The animation above shows that a circle can be cut and rearranged to closely resemble a parallelogram of area pi times the square of the radius. By dividing the circle into more than eight slices, the approximation obtained in this manner would be even better. By dividing the circle into more and more slices, the approximating parallelograms approximate the area of the circle arbitrarily close. This give a geometric justification that the area of a circle really is "pi r squared". When we have the length of the diameter or the radius or the circumference of the circle, we can find the surface area of the circle by using the surface area formula.

This surface area of the circle is represented in terms of square units. Fill the circle with radius r with concentric circles. After cutting the circle along the indicated line in fig. 4 and spreading the lines, the result will be a triangle. The base of the triangle will be equal to the circumference of the circle, and its height will be equal to the radius of the circle. For those having difficulty using formulas manually to find the area, circumference, radius and diameter of a circle, this circle calculator is just for you.

The equations will be given below so you can see how the calculator obtains the values, but all you have to do is input the basic information. The area of a circle can be thought of as the number of square units of space the circle occupies. This can be found using either the radius or the diameter, which we will cover in the examples below. We will also look at some examples of word problems involving area that you may come across in your studies. If you know the circumference, radius, or diameter of a circle, you can also find its area.

Area represents the space enclosed within a circle. It's given in units of distance squared, such as cm2 or m2. In this lesson, we will look at finding the area, the perimeter, and the radius of a quarter circle.

Knowing how to find these key pieces of information for quarter circles will serve you well as you advance in your math classes and as you take standardized math tests. Not only will you find these types of problems on math tests, but you may also find these types of problems working as an architect or as an engineer. An area of a circle is defined as a space occupied by the circle in a two-dimensional plane.A circle is an important geometric figure. We see circular objects around us in our everyday life, such as a bangle, a coin, a bike wheel, etc. To know more about circles, we must understand the terms related to circles, like radius, diameter, perimeter, area of the circle, etc. One such important parameter, the area of a circle, is the region occupied by a circle in two dimensions.

In geometry, a circle is a set of all points in a plane that have the same distance to a point called the center of the circle. In other words, a circle is a locus of coplanar points equidistant from a certain point called the center. Coplanar points are points located in a plane. The distance from any point of the circle to its center is called the radius.

We used to view a circle as a round line or figure. However, a circle looks round only in Euclidean geometry. In some metric spaces, for example in the taxicab or Chebyshev's spaces the circles look rather square. The perimeter and area of triangles, quadrilaterals , circles, arcs, sectors and composite shapes can all be calculated using relevant formulae.

The circle is divided into 16 equal sectors, and the sectors are arranged as shown in fig. The area of the circle will be equal to that of the parallelogram-shaped figure formed by the sectors cut out from the circle. Since the sectors have equal area, each sector will have an equal arc length. The red coloured sectors will contribute to half of the circumference, and blue coloured sectors will contribute to the other half.

If the number of sectors cut from the circle is increased, the parallelogram will eventually look like a rectangle with length equal to πr and breadth equal to r. The area of the circle is the measure of the space or region enclosed inside the circle. In simple words, the area of a circle is the total number of square units inside that circle. To understand how to calculate square footage we must first begin with the definition of area. An area is the size of a two-dimensional surface. The area of a circle is the space contained within its circumference .

To find out the area of a circle, we need to know its diameter which is the length of its widest part. The diameter should be measured in feet for square footage calculations and if needed, converted to inches , yards , centimetres , millimetres and metres . Apply basic right-angle trigonometry to learn about the relationships among steepness, angle of elevation, and height-to-distance ratio. Use trigonometric ratios to solve problems involving right triangles. This week your student will learn why circles are different from other shapes, such as triangles and squares.

Circles are perfectly round because they are made up of all the points that are the same distance away from a center. And this area of a disk is more often called the area of a circle. In many other languages, there is no such ambiguity. The area of a circle can be also described as the number of square units needed to cover the surface of a disk surrounded by a circle. We have discussed till now the different parameters of the circle such as area, perimeter or circumference, radius and diameter.

Let us solve some problems based on these formulas to understand the concept of area and perimeter in a better way. As we know, the area of circle is equal to pi times square of its radius, i.e. π x r2. To find the area of circle we have to know the radius or diameter of the circle. This area is the region that occupies the shape in a two-dimensional plane.

Now we will learn about the area of the circle. So the area covered by one complete cycle of the radius of the circle on a two-dimensional plane is the area of that circle. Now how can we calculate the area for any circular object or space? In this case, we use the formula for the circle's area. The answer will be square units of the linear units, such as mm2, cm2, m2, square inches, square feet, and so on.

The surface area and volume of a cylinder and cone with circular bases contain the formula for area of circle. The lateral surface of a cone consists of all segments that connect the vertex with points on the base. If we cut it along the slant height then the lateral surface is the sector of a circle.

So, the lateral area of a cone also uses the formula for area of circle. Area and circumference of circle calculator uses radius length of a circle, and calculates the perimeter and area of the circle. It is an online Geometry tool requires radius length of a circle. Using this calculator, we will understand methods of how to find the perimeter and area of a circle. A quarter-circle is formed by taking one part of a circle which has been equally divided into four.

Learn about the quarter circle and understand how to calculate its area, perimeter, and radius. The perimeter of a closed figure is known to be the length of its total boundary. When it comes to the circles, the perimeter is called by a different name.

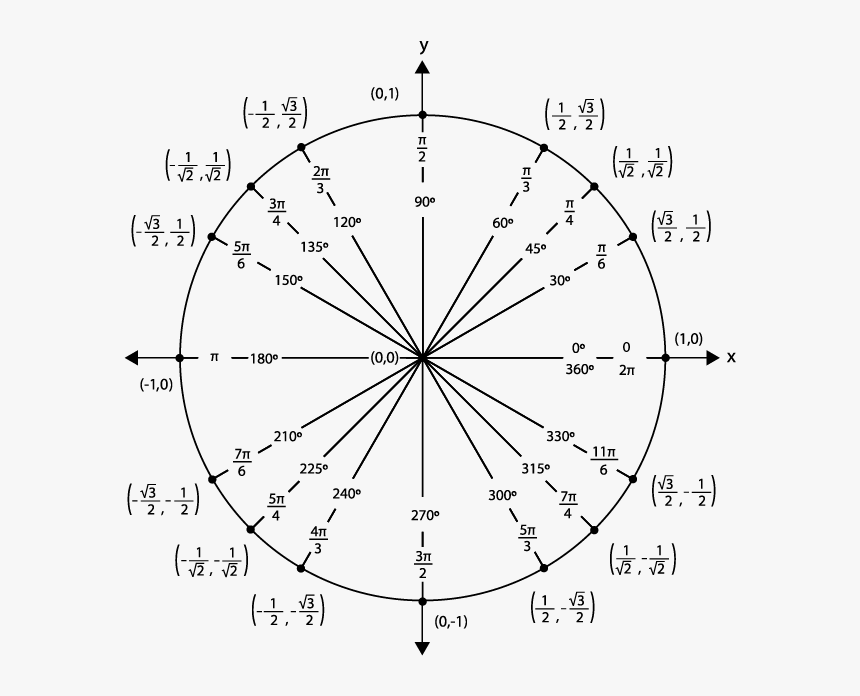
It is referred to as the 'circumference' of the given circle. This circumference is known as the total length of the boundary of the given circle. If we open the circle and form a straight line, the length of the straight line that we get is the circumference. For defining the circumference of a circle, we need to know a term called 'pi'. Consider the circle shown below having its centre at O and radius r.

We use this formula to measure the space which is occupied by either a circular plot or a field. In this article today, we will discuss the area of circle definition, the area of a circle equation, its circumference and surface area in detail. In this method, we divide the circle into 16 equal sectors.

The sectors are arranged in such a way that they form a rectangle. All sectors are similar in area, so hence all sectors' arc length would be equal. The circle's area would be the same as the area of the parallelogram shape or rectangle. Only a mathematician can genuinely understand the practical importance of formulas for calculating area, radius, diameter, or circle circumference.

While most people think that formulas have no practical use, they are critical factors in many everyday life routines. The first step for calculating the area of a circle from its diameter is to find that diameter. While math problems often list this value, in the real world, you must find the diameter yourself. The diameter is the length of a line that begins at the edge of the circle, passes through the center of the circle, and ends at the opposite edge of the circle. To measure, you will need a ruler for small circles or a tape measure for large circles. The perimeter of circle is nothing but the circumference, which is equal to twice of product of pi (π) and radius of circle, i.e., 2πr.

Area of a circle is the region covered or enclosed within its boundary. In technical terms, a circle is a locus of a point moving around a fixed point at a fixed distance away from the point. Basically, a circleis a closed curve with its outer line equidistant from the center. The fixed distance from the point is the radius of the circle.

In real life, you will get many examples of the circle such as a wheel, pizzas, a circular ground, etc. Now let us learn, what are the terms used in the case of a circle. Both area and perimeter can be calculated with simple formulas using the radius or diameter of the circle and the value of pi. If the area of the circle is not equal to that of the triangle, then it must be either greater or less. We eliminate each of these by contradiction, leaving equality as the only possibility. A set of points in a plane equally distanced from a given point $O$ is a circle.

The point $O$ is called the center of the circle. The distance from the center of a circle to any point on the circle is called the radius of this circle.A radius of a circle must be a positive real number. The circle with a center $O$ and a radius $r$ is denoted by $c$. The area of a circle is the total number of square units that fill the circle. The area of the following circle is about 13 units.

Note that we count fractional units inside the circle as well as whole units. In this program, the radius of the circle is obtained from the user. Then the radius is converted to float using the float() method. Then the input() method is used for fetching the units of measurement from the user, that can be in cm or inches.

Session 7 Circles and Pi (π) Investigate the circumference and area of a circle. Examine what underlies the formulas for these measures, and learn how the features of the irrational number pi (π) affect both of these measures. Learn about the many uses of ratio in measurement and how scale models help us understand relative sizes. Investigate the constant of proportionality in isosceles right triangles, and learn about precision and accuracy in measurement.

The standard deviation of 25 sheets of paper is just 0.5% of the mass of the sheet. If I cut out circles of different diameters and measure the mass of the circle then I can calculate the area. If the area is also supposed to be πR2, I can make a plot of area vs. diameter squared. A circle is a perfect shape because every part of the circle is the same distance from its center. Some consider it the most perfect of figures. Like other perfect shapes, a circle is often used in architecture.